|

Solving of Sudoku puzzles with logical Algebra.
Solving a Sudoku puzzle is often a right Baste lei. If you finally have finished ,
eventually the last number will not fit, and you have to start all over again. In the following text, a solution method is described who is based on logical
comparison. This method will without complicated formula calculation always lead to the solution.This method comes from digital electronics.
1. The puzzle.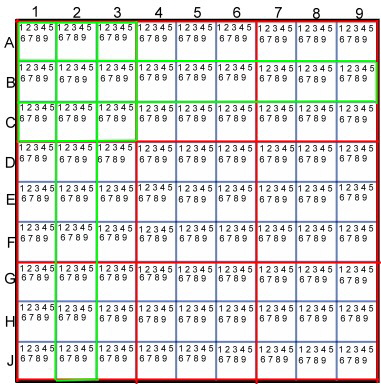
Fig.1 shows the puzzle, it has 9 rows (A-J) and 9 columns. (1-9) Each row has nine fields, and each column has nine
fields, for a total of 81 fields.The 3 rows and 3 columns forming a square, also with 9 fields. Each column, each row, and the corresponding square form a unit SZQ.
Fig.1 Empty Sudoku for computing the solution
A SZQ - example in Figure 1 is drawn in green. In the solved puzzles, all
numbers from 1-9 can be in every row, every column, and every square.These target numbers of the OR - condition is indicated in Figure 1, with
small numbers in each field. At the beginning of the puzzle is already in some fields one of this numbers, not in others. In such fields, the small letters
numbers no longer apply, of course.The puzzle is solved if there are in each row and each column and in the squares one of the numbers 1-9.Then
account for all numbers the small letters. In a real puzzle, these figures are not available, because this fact is well known. But to understand the solution
path, it is convenient if these auxiliary digits are available.The calculation goal is not the direct computation of the solution, but we reduce by means of
logical comparison the small target figures, until there comes a solution by itself.
2.The solution method
We solve the puzzle using four logical comparisons: YES / NO, TRUE /
FALSE and OR.
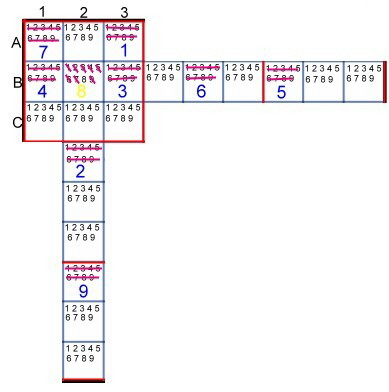 In Figure 2 there is a SZQ with specified numbers. Of course, in these known fields, the small target numbers are no longer valid, this
field is completed. Now let's break down the field B 2. We ask yes /no , for this field from the SZQ and find: 1 not ( cross out this number ), 2 not, 3 not, 4 not ,5 not, 6
not, 7 not, 9 not. In Figure 2 there is a SZQ with specified numbers. Of course, in these known fields, the small target numbers are no longer valid, this
field is completed. Now let's break down the field B 2. We ask yes /no , for this field from the SZQ and find: 1 not ( cross out this number ), 2 not, 3 not, 4 not ,5 not, 6
not, 7 not, 9 not.
Fig.2 SZQ The Comparison Yes/No
Now all the numbers are crossed 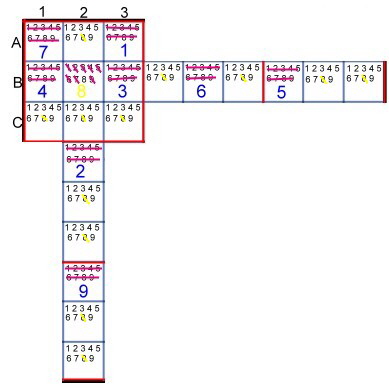 out except for the 8, ergo the solution can mean only 8. If the solution is not obtained, because for example, the 6 would not exist, yet we have reduced a
lot of target figures. The solution is then obtained sometime in the course of degradation. And the degradation proceeds immediately because the found 8 builds away all remaining 8 from
the SZQ.These are streaked yellow in Figure 3. out except for the 8, ergo the solution can mean only 8. If the solution is not obtained, because for example, the 6 would not exist, yet we have reduced a
lot of target figures. The solution is then obtained sometime in the course of degradation. And the degradation proceeds immediately because the found 8 builds away all remaining 8 from
the SZQ.These are streaked yellow in Figure 3.
Fig. 3 Degradation of target figures found by solution
Figure 4 shows the SZQ with a very different situation. 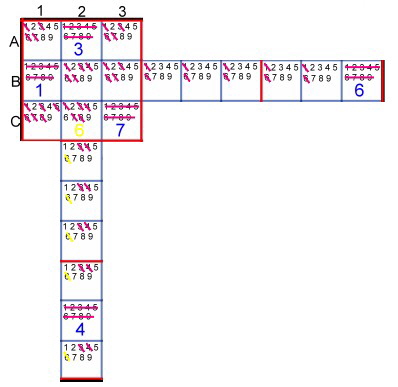 As we had practised in the last example, we cross out the 6 and the 1 in the
line, and the 3 and the 4 in column as well as the 1, 3 and 7 in the square. Now we ask all remaining numbers in the square, whether they are TRUE or FALSE. Wrong they are when
they occur in the square at least 2 times.True they are, if they are present only once in the square. As we had practised in the last example, we cross out the 6 and the 1 in the
line, and the 3 and the 4 in column as well as the 1, 3 and 7 in the square. Now we ask all remaining numbers in the square, whether they are TRUE or FALSE. Wrong they are when
they occur in the square at least 2 times.True they are, if they are present only once in the square.
Fig. 4 Target number degradation by true and false
From other degradation, the number 6 has been already deleted in all fields,
but not in C2. We immediately delete the 6 in column 2. The same question game you can carry out for the row and the column. Finally, one can perform
this query, for all the target numbers on all fields and SZQ's. Every new solution found yields new deleting opportunities until all desired numbers
are deleted. But if all the numbers can not be broken, then what? Then helps the OR test. With two remaining digits, only one can be the solution. Does
the attempt to no solution, it may be just the other digit. In practice, the OR test is usually not necessary.
Have fun.
|